10.2 Review of E&M #
Homework group: just me n leek42@uw.edu
Realistically, all of the E&M review comes from https://peppyhare.github.io/griffiths-em/
10.1.1 Maxwell Stress Tensor #
The Maxwell stress tensor encompasses the way that electromagnetic fields an exert forces/stresses in 3D space:
\[\vec p = \text{ momentum }\]The basic force laws of E&M are
\[\dv{\vec p}{t} = q \left( \vec E + \vec v \cross \vec B \right)\]On an element of volume, the change in momentum is
\[\dv{P}{t} = \int_V (\rho E + j \cross B) \dd V\]The maxwell equations give the source terms as
\[\rho = \epsilon _0 \div \vec E \qquad \vec j = \frac{1}{\mu_0} \left( \curl \vec B - \mu_0 \epsilon_0 \pdv{E}{t} \right)\] \[\rho \vec E + \vec j \cross \vec B = \vec E \epsilon_0 (\div E) - \frac{B}{\mu_0} \cross ( \curl B - \mu_0 \epsilon_0 \pdv{E}{t} )\]Using the chain rule \( \pdv{}{t} (E \cross B) = \pdv{E}{t} \cross B + E \cross \pdv{B}{t} \) and \( B( \div B) = 0 \)
\[\rho E + j \cross B = \epsilon_0 E( \div E) - \frac{B \cross (\curl B)}{\mu_0} + \epsilon_0 \left[ E \cross \pdv{B}{t} - \pdv{}{t} (E \cross B) \right]\]From Faraday, \( \pdv{B}{t} \rightarrow \curl E \)
\[= \epsilon_0 E(\div E) + \frac{B(\div B)}{\mu_0} - \frac{B \cross (\curl B)}{\mu_0} - \epsilon_0 E \cross (\curl E) - \epsilon_0 \pdv{}{t} (E \cross B)\]Finally we’ve got everything in place to use the identity
\[\frac{1}{2} \grad (B^2) = \frac{1}{2} \grad (\vec B \cdot \vec B) = (\vec B \cdot \grad) \vec B + \vec B \cross (\curl \vec B)\]All together,
\[\rho E + j \cross B = \epsilon_0 \left[ E ( \div E ) + (\vec E \cdot \grad) E - \frac{1}{2} \grad (E^2) \right] + \frac{1}{\mu_0} \left[B (\div B) + (\vec B \cdot \grad) B - \frac{1}{2} \grad (B^2) \right] - \epsilon_0 \pdv{}{t} ( \vec E \cross \vec B)\]Integrating over a volume,
\[\dv{P}{t} + \epsilon_0 \pdv{}{t} \int \vec E \cross \vec B \dd V\] \[\qquad = \int \epsilon_0 \left[ E(\div E) + (E \cdot \grad) E - \frac{1}{2} \grad(E^2) \right] + \frac{1}{\mu_0} \left[ B(\div B) + (B \cdot \grad) B - \frac{1}{2} \grad (B^2) \right] \dd V\]To simplify, we use another identity
\[E (\div E) + (E \cdot \grad) E - \frac{1}{2} \grad (E^2) = \div (\vec E \vec E - \frac{1}{2} \vec 1 E^2)\]And the same is true for \( \vec B \). The momentum change expression is simplified if we define the Maxwell stress tensor as
\[\vec T = \epsilon_0 \vec E \vec E + \frac{\vec B \vec B}{\mu_0} - \frac{1}{2} \vec 1 \left( \epsilon_0 E^2 + \frac{B^2}{\mu_0} \right)\]That lets us re-cast the momentum change in a volume as a stress tensor on a surface
\[\dv{\vec p}{t} + \epsilon_0 \dv{}{t} \int ( \vec E \cross \vec B) \dd V = \int \div \vec T \dd V = \int \vec T \cdot \vu{n} \dd \vec a\]Example: Application to FRC (Field-Reversed Configuration) #
In a FRC confinement experiment, a bias field \( B_{\infty} \) is applied and quickly reversed, resulting in poloidal fields opposite the bias current.
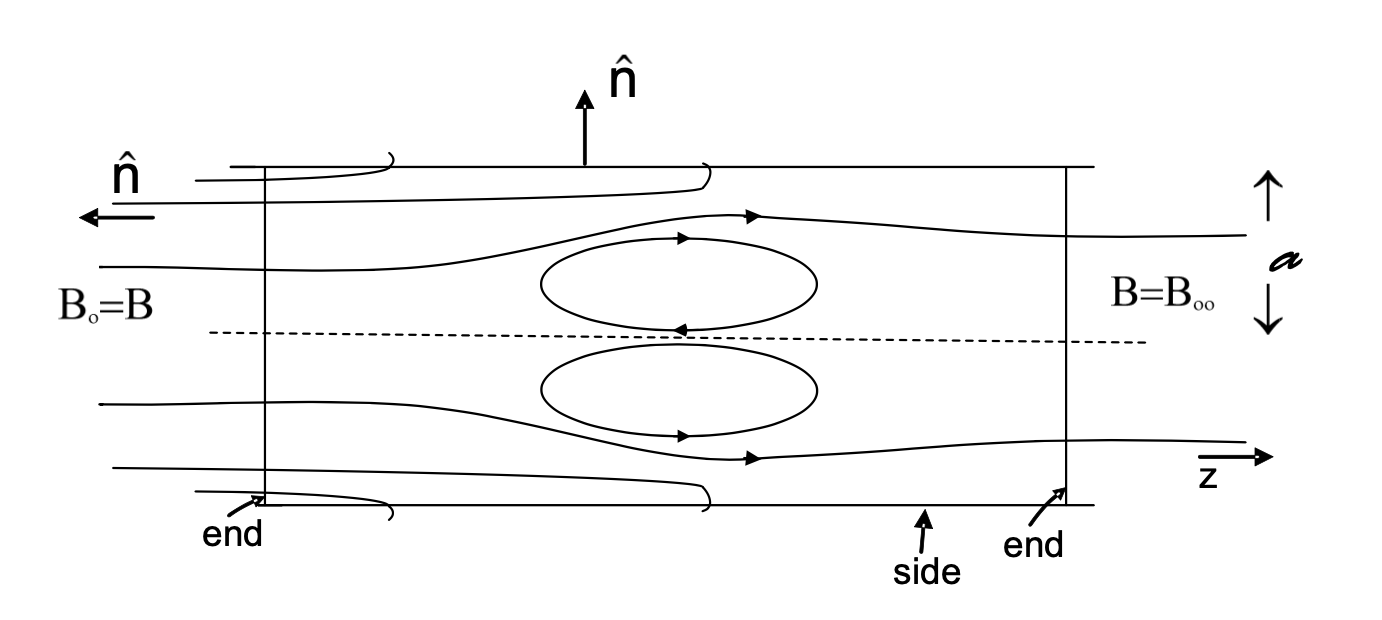
If we want to confine a plasma in the center of the FRC, we want to calculate the force on our plasma (electron fluid).
\[\vec F = \int \vec T \cdot \vu n \dd a\]At the left end of the configuration where we have \( \vec B = B_z \vu z \) and we define \( B_1 = B_r, B_2 = B_z, B_3 = B_\theta \)
\[\vec T = \begin{bmatrix} - \frac{1}{2} \frac{B_0 ^2}{\mu_0} & 0 & 0 \\ 0 & \frac{B_0 ^2}{\mu_0} - \frac{1}{2} \frac{B_0 ^2}{\mu_0} & 0 \\ 0 & 0 & - \frac{1}{2} \frac{B_0 ^2}{\mu_0} \end{bmatrix}\] \[\vec T \cdot \vu n = \begin{bmatrix} 0 \\ -\frac{1}{2} \frac{B_0 ^2}{\mu_0} \vu z \\ 0 \end{bmatrix}\]Now what about at the sides? There, \( B_r \neq 0 \) and
\[\vec T \cdot \vu n = \begin{bmatrix} - \frac{1}{2} \frac{B^2}{\mu_0} + \frac{B_r ^2}{\mu_0} & \frac{B_r B_z}{\mu_0} & 0 \\ \frac{B_r B_z}{\mu_0} & - \frac{1}{2} \frac{B^2}{\mu_0} + \frac{B_z ^2}{\mu_0} & 0 \\ 0 & 0 & - \frac{1}{2} \frac{B^2}{\mu_0} \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} = \begin{bmatrix} - \frac{1}{2} \frac{B^2}{\mu_0} + \frac{B_r ^2}{\mu_0} \\ \frac{B_r B_z}{\mu_0} \\ 0 \end{bmatrix}\]The total force is the sum
\[\vec F = \int \vec T \cdot \vu n \dd a = \left( - \frac{1}{2} \frac{B_0 ^2}{\mu_0} + \frac{1}{2} \frac{B_{0} ^2}{\mu_0} \right) \pi a ^2 \vu z + \text{ contrib. from sides}\]By symmetry, the \( r \) components add to zero
\[F_z = \frac{\pi a^2}{2 \mu_0} (B_{\infty} ^2 - B_0 ^2) + \frac{2 \pi a}{\mu_0} \int B_r B_z \dd z\]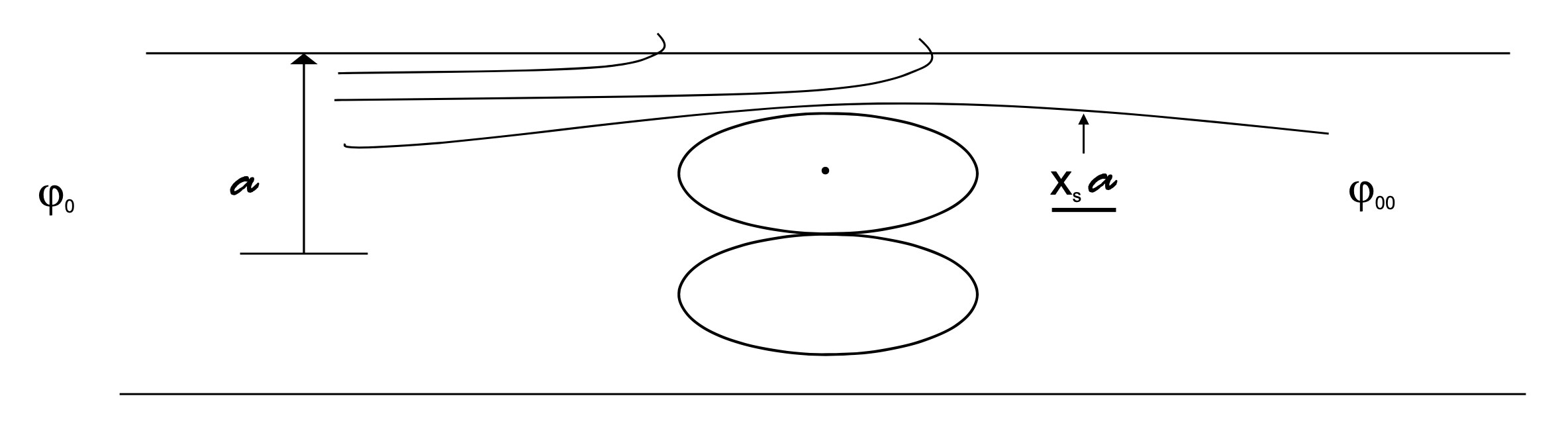
The magnetic flux at the open ends must go somewhere
\[\Phi = B_z \pi a^2 (1 - x_s ^2) \] \[2 \pi a B_r \dd z = - \dd \Phi\] \[F_z = \frac{1}{2 \mu_0 \pi a^2} ( \Phi_{\infty} ^2 - \Phi_0 ^2 ) - \frac{1}{\mu_0 } \int_{\Phi_0} ^{\Phi_{\infty}} \frac{\Phi}{\pi a^2 ( 1 - x_s ^2)} \dd \Phi\]Assume \( x_s \) is constant (or that it is an appropriate average value)
\[F_z = \frac{1}{2 \mu_0 \pi a^2} ( \Phi_{\infty} ^2 - \Phi_0 ^2 ) - \frac{ \Phi_{\infty} ^2 - \Phi_0 ^2}{2 \mu_0 \pi a ^2 (1 - x_s ^2)}\] \[= \frac{\pi a^2}{2 \mu_0} ( B_\infty ^2 - B_0 ^2) \left( 1 - \frac{1}{1 - x_s ^2} \right)\] \[= \frac{\pi a^2}{2 \mu_0 } ( B_0 ^2 - B_{\infty} ^2 ) \frac{x_s ^2}{1 - x_s ^2}\] \[= \frac{A_{frc}}{2 \mu_0} ( B_0 ^2 - B_{\infty} ^2 ) \left( \frac{1}{1 - x_s ^2} \right)\]Where \( A_{frc} = \pi a^2 x_s^2 \) is the cross-sectional area of the FRC. So, in the simple picture the force is the same as the initial flux, reduced by an equivalent area of the FRC torus.