Equilibrium of 3D Configurations#
In 3 dimensions, we lose the axisymmetry that allowed us to reach the Grad-Shefranov equation and we need to solve the full momentum equation in three dimensions. This is not something that we can actually do in this class, and the existing codes that do this are quite sophisticated.
Some general features of 3D equilibria are:
- No net toroidal current. This means that they tend to be steady-state configurations.
- Radial confinement is accomplished by toroidal fields, as in the end-connected \( \theta \) -pinch. As we saw, toroidal fields cannot provide radial confinement in a purely axisymmetric configuration, but radial variation with \( \phi \) can provide confinement.
- Toroidal effect (radial force balance) is generated by helical magnetic fields. You can do an expansion of the magnetic field into a toroidal component, and a helical component that traces out a twisted shape as you move around the torus. These twisted shapes are what lead to radial confinement.
ELMO Bumpy Torus (EBT)#
In contrast to most other 3D configurations, even though the EBT is a 3D equilibrium, it has no helical windings.
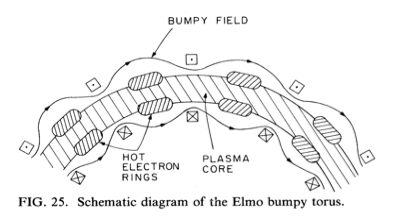
Since there are no helical windings, we have to provide radial stability in another way. In the EBT configuration, you also drive hot poloidal electron rings (driven by electron cyclotron resonance) to provide both stability and heating.
Stellarator#
The stellarator configuration is composed of a number of helical current lines (generated by helical coils with alternating currents), and a net toroidal field driven by poloidal coils. The direction of the currents alternate, for a total of \( 2l \) current lines.
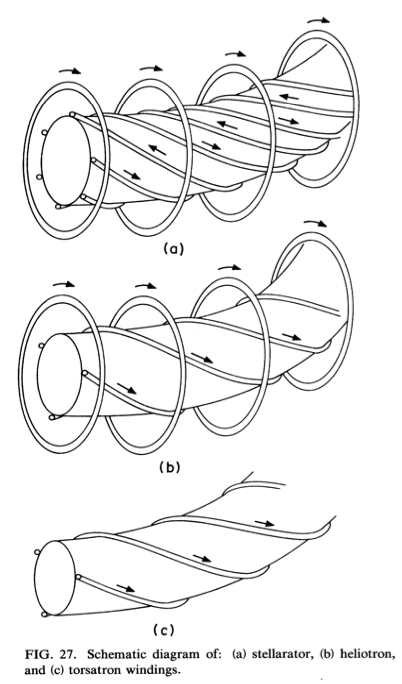
The result is a net magnetic field with a ratio such that \( B_{\text{helical}} \gg B_\phi \)
Stellarators raise some very complicated engineering challenges both in the design and construction of the complicated geometry. It is also very difficult to maintain no net current within the plasma, especially during start-up. As you add plasma, you raise from zero \( \beta \) to a finite \( \beta \) , introducing things like bootstrap currents that need to be balanced.
Torsatron#
Similar to a stellarator, the torsatron does not have alternating currents. All of the helical current lines are in the same direction. There are also no toroidal field coils.
The engineering is slightly simpler, but it is slightly less efficient at generating the helical magnetic field.
The flux surfaces in stellarators and torsatrons have geometrical cross-sections depending on the number \( l \) of helical current lines. About the current lines, the flux surfaces are nearly circular. The flux surfaces within the plasma volume are determined by the separatrix of the helical coil fields.
