Chapter 5 Solved Problems #
\[\]Problem 5.5 #
K is the current per unit width \( \perp \) to the direction of the flow.
\[K = \frac{I}{2 \pi a} \]Suppose instead the current is distributed somehow throughout the volume of the wire such that the current density is inversely proportional to the distance from the axis. Then
\[j = \frac{\text{current}}{\text{unit area } \perp \text{ flow}} = \frac{d I}{da_{\perp}} \]We suppose that j has the form
\[j = \frac{\text{const.}}{s} = \frac{c}{s} \] \[\begin{aligned} I & = \int j \dd a_{\perp} \\ & = \int_{0} ^a \int_{0} ^{2 \pi} \frac{c}{s} s \dd s \dd \phi \\ & = 2 \pi c a \end{aligned}\]so
\[c = \frac{I}{2 \pi a} \]and
\[j = \frac{I}{2 \pi a s} \]Problem 5.11 #
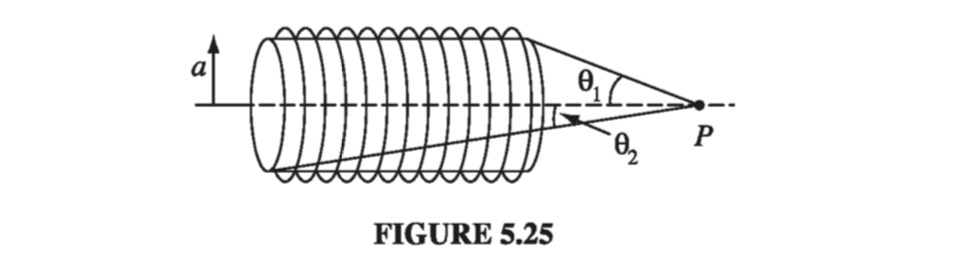
If I have n turns per unit length, then I have \( n \dd z \) turns along a length \( \dd z \) (using the natural cylindrical coordinates of the problem). The total current of the resulting loop is \( I n \dd z \). From Ex 5.6, we know the magnetic field due to a circular loop is
\[\dd \vec{B}(z) = \frac{ \mu_0 n I \dd z}{2} \frac{a^2}{(a^2 + z^2 )^{3/2}} \vu{\phi} \]From the geometry of Fig 5.25,
\[\tan \theta = \frac{a}{z} \quad \rightarrow \quad z = \frac{a}{\tan \theta} \] \[\dd z = - \frac{a}{\sin ^2 \theta} \dd \theta\] \[(a^2 + z^2)^{3/2} = \left( a^2 + \frac{a^2}{\tan ^2 \theta} \right)^{3/2} = \left( \frac{a}{\sin \theta} \right)^3\] \[\begin{aligned} B(z) & = \frac{\mu_0 n I}{2} \left( - \frac{a}{\sin ^2 \theta} \dd \theta \right)\frac{a^2}{(a^3 / \sin ^3 \theta)} \\ & = - \frac{\mu_0 n I}{2} \sin \theta \dd \theta \end{aligned}\] \[\begin{aligned} B(z) & = - \frac{\mu_0 n I}{2} \int _{\theta_1} ^{\theta_2} \sin \theta \dd \theta \\ & = \frac{\mu_0 n I}{2} (\cos \theta_2 - \cos \theta_1) \end{aligned}\]For an infinite solenoid, we get
\[B(z) = \frac{\mu_0 n I}{2} (\cos(0) - \cos \theta_1)\]Problem 5.23 #
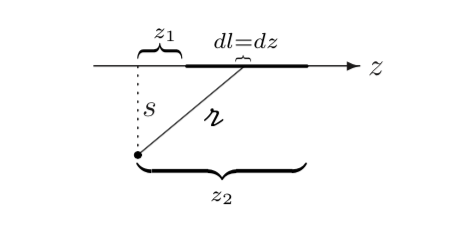
We will get our vector potential using Eq 5.66, as suggested
\[\begin{aligned} \vec{A} & = \frac{\mu_0 }{4 \pi} \int \frac{I \vu{z}}{\gr} \\ & = \frac{\mu_0 I}{4 \pi} \vu{z} \int _{z_1} ^{z_2} \frac{dz}{\sqrt{z^2 + s^2}} \\ & = \left. \frac{\mu_0 I}{4 \pi} \vu{z} \left[ \ln \left( z + \sqrt{z^2 + s^2} \right) \right] \right|_{z_1} ^{z_2} \\ & = \frac{\mu_0 I}{4 \pi} \ln \left( \frac{z_2 + \sqrt{(z_2)^2 + s^2}}{z_1 + \sqrt{(z_1)^2 + s^2}} \right) \vu{z} \end{aligned}\]To get the magnetic field, we need to take the curl of A. We can easily tell from the symmetry of the problem that the field will be “circumferential” (in the \( \vu{\phi} \) direction):
\[\begin{aligned} \vec{B} & = \curl \vec{A} = - \pdv{A}{s} \vu{\phi} \\ & = - \frac{\mu_0 I}{4 \pi} \left( \frac{1}{z_2 + \sqrt{(z_2)^2 + s^2}} \frac{s}{\sqrt{(z_2)^2 + s^2}} - \frac{1}{z_1 + \sqrt{(z_1)^2 + s^2}} \frac{s}{\sqrt{(z_1)^2 + s^2}} \right) \vu{\phi} \\ & = - \frac{\mu_0 I s}{4 \pi} \left( \frac{z_2 - \sqrt{z_2 ^2 + s^2}}{z_2 ^2 - (z_2 ^2 + s^2)} \frac{1}{\sqrt{z_2 ^2 + s^2}} - \frac{z_1 - \sqrt{z_1 ^2 + s^2}}{z_1 ^2 - (z_1 ^2 + s^2)} \frac{1}{\sqrt{z_1 ^2 + s^2}} \right) \vu{\phi} \\ & = - \frac{\mu_0 I s}{4 \pi} \left( - \frac{1}{s^2} \right) \left( \frac{z_2}{\sqrt{z_2 ^2 + s^2}} - 1 - \frac{z_1}{\sqrt{z_1 ^2 + s^2}} + 1 \right) \vu{\phi} \\ & = \frac{\mu_0 I}{4 \pi s} \left( \frac{z_2}{\sqrt{(z_2) ^2 + s^2}} - \frac{z_1}{\sqrt{z_1 ^2 + s^2}} \right) \vu{\phi} \end{aligned}\]or, in terms of the angles made between r and the axis of the wire,
\[\sin \theta_1 = \frac{z_1}{\sqrt{z_1 ^2 + s^2}} \quad \text{ and } \quad \sin \theta_2 = \frac{z_2}{\sqrt{z_2 ^2 + s^2}} \] \[\vec{B} = \frac{\mu_0 I}{4 \pi s} (\sin \theta_2 - \sin \theta_1) \vu{\phi} \]which is just what we got back in Eq. 5.37.
Problem 5.26 #
(a) By whatever means you can think of (short of looking it up), find the vector potential a distance \( s \) from an infinite straight wire carrying a current \( I \). Check that \( \div \vec{A} = 0 \) and \( \curl \vec{A} = \vec{B} \).
(b) Find the magnetic potential inside the wire, if it has radius R and the current is uniformly distributed.
(a) As we said, because the current distribution is infinite, we cannot use Eq. 5.65 to get A. So let’s use some symmetry. A must be parallel (or antiparallel) to I, and is a function of only s (the distance from the wire). In cylindrical coordinates, then, \( \vec{A} = A(s) \vu{z} \). We already calculated the magnetic field of an infinite straight wire via Biot-Savart:
\[\vec{B} = \frac{\mu_0 I}{2 \pi s} \vu{\phi}\]We can work backwards to get A from B in this case.
\[\vec{B} = \curl \vec{A} = - \pdv{A}{s} \vu{\phi} = \frac{\mu_0 I}{2 \pi s} \vu{\phi}\]Therefore
\[\pdv{A}{s} = -\frac{\mu_0 I}{2 \pi s} \quad \rightarrow \quad \vec{A}(r) = - \frac{\mu_0 I}{2 \pi} \ln (s / a) \vu{z}\]There is an arbitrary constant a here which doesn’t actually affect our gauge at all:
\[\div \vec{A} = \pdv{A_z}{z} = 0\] \[\curl \vec{A} = - \pdv{A_z}{s} \vu{\phi} = \frac{\mu_0 I}{2 \pi s} \vu{\phi} = \vec{B}\](b) Ampere’s law in this case says
\[\oint \vec{B} \cdot \dd \vec{l} = B 2 \pi s = \mu_0 I_{enc} = \mu_0 J \pi s^2 = \mu_0 \frac{I}{\pi R^2} \pi s^2 = \frac{\mu_0 I s^2}{R^2} \]so, inside the wire,
\[\vec{B} = \frac{\mu_0 I s}{2\pi R^2} \vu{\phi}\]From the definition of A,
\[\pdv{A}{s} = - \frac{\mu_0 I}{2 \pi} \frac{s}{R^2} \rightarrow \vec{A} = -\frac{\mu_0 I}{2 \pi R^2} \int_{b} ^s s \, \dd s = - \frac{\mu_0 I}{4 \pi R^2} (s^2 - b^2) \vu{z}\]Here, again, b is arbitrary, except that A must be continuous at R (we know that A is continuous!)
\[- \frac{\mu_0 I}{2 \pi } \ln (R / a) = - \frac{\mu_0 I}{4 \pi R^2} (R^2 - b^2)\]which means that we have to pick a and b such that
\[2 \ln (R / b) = 1 - (b / R)^2\]One such combination of a and b is \( a = b = R \). Then
\[\vec{A} = \begin{cases} - \frac{\mu_0 I}{4 \pi R^2} (s^2 - R^2) \vu{z} & \quad \text{ for } s \leq R \\ - \frac{\mu_0 I}{2 \pi} \ln(s / R) \vu{z}& \quad \text{ for } s \geq R \end{cases}\]Problem 5.37 #
(a) A phonograph record of radius R, carrying a uniform surface charge \( sigma \) is rotating at constant angular velocity \( \omega \). Find its magnetic dipole moment.
(b) Find the magnetic dipole moment of the spinning spherical shell in Example 5.11. Show that for points \( r > R \) the potential is that of a perfect dipole.
(a) We get the monopole moment by integrating over the disk of the record. For a ring at radius r, \( m = I \pi r^2 \). In this case,
\[I \rightarrow \sigma v \dd r = \sigma \omega r \dd r\]so
\[m = \int _0 ^R \pi r^2 \sigma \omega r \dd r = \pi \sigma \omega R^4 / 4\](b) To get the magnetic dipole moment of our sphere, we need to integrate over the surface of the sphere:
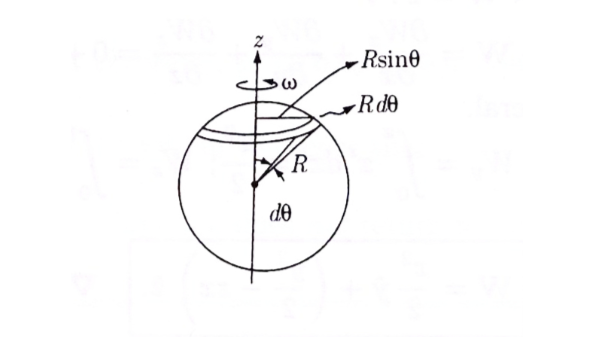
The area of the ring is \( \pi (R \sin \theta)^2 \), so the magnetic moment of the ring is
\[\dd m = (\sigma \omega R^2 \sin \theta \dd \theta) \pi R^2 \sin ^2 \theta\]and the total dipole moment is
\[m = \sigma \omega \pi R^4 \int_0 ^\pi \sin ^3 \theta \dd \theta = (4 / 3) \sigma \omega \pi R^4\]and we know that m points in the \( \vu{z} \) direction (right-hand-rule), so
\[\vec{m} = \frac{4 \pi}{3} \sigma \omega R^4 \vu{z}\]The dipole term in the multipole expansion for A is therefore
\[\vec{A}_{dip} = \frac{\mu_0}{4 \pi} \frac{4 \pi}{3} \sigma \omega R^4 \frac{\sin \theta}{r^2} \vu{\phi} = \frac{\mu_0 \sigma \omega R^4}{3} \frac{\sin \theta}{r^2} \vu{\phi}\]This is actually the exact vector potential we calculated (Eq. 5.69); evidently a spinning sphere produces a perfect dipole field, with no higher multipole contributions.